- cross-posted to:
- memes@lemmy.ml
- cross-posted to:
- memes@lemmy.ml
Explanation (which might be wrong, since I’m writing this after banging my head against a wall. Please do correct me if I’m wrong):
In regular numbering systems (i.e., decimal), we exhaust all 10 digits (0–9) before we reach two-digit numbers. The first number to require 3 digits is 10². The first to use 4 is 10³, and so on.
In music intervals, there is no “0”. The interval c’–c’, for instance, is called a prime (1). This has the funny consequence that moving by a fifth and then by a fourth doesn’t land you on the ninth, but the octave (8). Moving by an octave and then another octave gets you to the 15th, not the 16th.
In Excel, shit hits the fan when you need to convert column names (A, B, C…) to numbers (0, 1, 2…). Since we use 26 characters as our ‘digits’, we’re in the hexavigesimal system. Knowing what I told you in the first paragraph, you’d expect the first double-digit column (AA) to be 26. And you’re right.
However, when do we need 3 digits? Which column is column AAA? A sane person would say it’s 26², so 676. Ha! No. Column number 676 is actually ZA. What gives? Well, we only ditch the zero for single digit numbers. All subsequent columns actually use 27 different characters, the ‘empty character’ being one of them. That’s where we get the ‘single digit’ – there actually is a second digit, only it’s empty.
So the column AAA actually has index 702, or 26×27. Which index does the column AAAA have? 26×27². The system of adding powers of the base works, only we changed bases midway through.
You can see the lopsidedness in the index lookup table (I’m not displaying all characters for brevity). Sane number systems have square tables. Excel’s is 26×27 (shown are 4×5).
You must log in or register to comment.
That’s…not how octaves work. I don’t know how to provide a constructive correction because I don’t understand what you’re saying about 15ths in the first place.
Could you elaborate? I’m a music teacher and it checks out to me.
C4 up a 5th is G4, then up a fourth is C5. C4 to C5 is an octave.
Two octaves is a 15th. In music when the composer wants you play up an octave, they write (typically) 8va. When they want you to play up two octaves, they write (typically) 15va.
People are focusing on the Excel part, I’ll focus on the maths.
I wish our societies picked base-12 instead of base-10. Divisions in base-12 give you repeating digits less often, and being able to split exactly by 3, 6, 9 and 12₁₀=10₁₂ is far more useful than doing it for 5 and 10₁₀=A₁₂.
Plus 4chan would stop arguing if 0.999… = 1. It would argue instead if 0.BBB… = 1.I wish our societies picked base-12 instead of base-10.
This, right here, is the hill I will die on. Imperial/US customary unit divisions are superior to metric decimalization.
Metric “dozenalisation” would be perfectly viable, and metric-dozenal units would still look nothing like USA units.
I’ll use length for the example. All of them in base 10, just for clarity. (Also the name of the units would be different, but I’m not changing them for this example.)
- metric-decimal: 10⁻³ km = 10⁻² hm = 10⁻¹ dam = 10⁰m = 10¹dm = 10²cm = 10³mm
- metric-dozenal: 12⁻³ km = 12⁻²hm = 12⁻¹ dam = 12⁰m = 12¹dm = 12²cm = 12³mm
- USA units: 1/1760mi = 1yd = 3ft = 3*12 in = 3*12*6 P = 3*12*6*12 p
Are you noticing what the USA units do? They don’t stick to a base.
What is with the spike in Excel related memes? I am out of the loop.
I think it’s a viral marketing campaign for the upcoming sequel “Excel 2”.
2Ex – 2Cells
Excel On The Beach by Kojima
excelectric boogaloo
I cannot imagine that a significant percentage of Excel power users care what column number ABC is. You use either A1 notation or R1C1 notation based on your need. You don’t have to convert between the two. You can even use the INDIRECT() function to reference a cell either way regardless of your general settings. In VBA, you can use Range(“A1”) or Cells(1,1) to reference cells with either notation. Either are always options. Conversion is not necessary.
This isn’t a question of functionality but just whether a system whether basic arithmetic, music, etc makes logical/intuitive sense.
Imperial measurements using feet, yards, mph, etc instead of metric centimeters, meters, kph, etc. Sure imperial works but it doesn’t make the same sense that metric does. Math can be done in base 2, base 60 or whatever it doesn’t make the same sense as base 10.
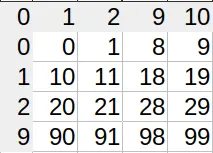
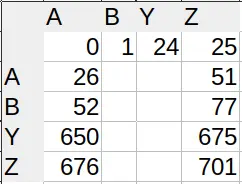
I’m a bit too tired and tipsy to fully wrap my head around this but I’m just as furious as you are!
This has the funny consequence that moving by a fifth and then by a fourth doesn’t land you on the ninth, but the octave (8). Moving by an octave and then another octave gets you to the 15th, not the 16th.
This is worded confusingly. The reason for this is simply because you include the base note when you start counting, so if you stop midway and stack another interval on top, you have to account for that stop because it decreases the total travel distance by one.
This is done to actually increase consistency. If you start at c1 and move up an octave and then move up another octave, you stop at c3 which is logical. So you either move 2 octaves or one 15th because 2*8-1 = 15.
Name the prime a “none”, the octave a sept.
Now, 2 “septaves”, c1 to c3, are a 14th. 2*7 = 14.You can make off-by-one intervals work, but you have to constantly juggle some +1s or -1s compared to what we usually use.
If you counted distance in steps, then moving from your front door to your front door would be 0 steps, not one, and moving by 6 steps is twice the distance of 3 steps.
A piano with 5 septaves has 5*7 = 60 keys, wait.
So anyway mathematically one dodecave, one 12th, c1 to c2, has 12 segments, the frequency diffefence is 2. So a second, 2 notes, has 2/12 of that interval, the ratio is 22/12.
A first, a halftone, has 21/12 as its frequency ratio, and a none has 20/12 = 1, the same frequency.No matter if you count physical keys, distance on a keyboard to change a note by, or mathematical frequency in the air, starting at 1 goes against our intuition, and when you try to add or multiply it is easy to get completely wrong results.
PS: You might want to go C to C on your 5 dodecave keyboard, in which case the concept of “started hour” etc. is familiar, you know to add one arriving at 61 keys, and you know that means an assymetry where one C doesn’t have 11 other keys to itself.
The other way around you’d have to subtract 4, so probably subtract 5 and add 1 since you were dealing with 5 tredecaves in your head not 1 base tredecave followed by 4 extension tredecaves.
This is a very fun implicit question!
First, in decimal, there are 10 symbols: 0-9. When we count from 0 to 9, the next number is 10, not 00 (which is equivalent to 0).
In base 26, there are 26 symbols (A-Z). If one wanted to use these symbols in the same way, A would be equivalent to 0, so 26 is represented by BA, not AA. However, if AA is not the same as A, then we can represent 26 as AA instead of BA.
Basically, in our typical numbering system, the leading digit can’t be 0, so there are 9×10 possible two digit numbers, and 10 possible single digit numbers. However, if the first digit can be 0, meaning, for example, if 03 is not the same as 3, there are 10×10 possible two digit numbers. This second approach is what excel and google sheets use. Column A is not the same as column AA. Hence, you start with single digit column numbers (A-Z). Then you move to two digit column numbers (AA-ZZ), of which there are 26². The last column before triple digits is column 26+26²=702. The first triple digit column number is 26+26²+1=703. Neat!
Comparing this to our system, the first 2 digit number is 10¹=10. The first 3 digit number is 10²=100. The first 4 digit number is 10³=1000.
Ok, I’m confused, is the blank actually used in the middle of large column labels? Like is “A A” a number? how about "A ", " A ", or even " "? (All are three characters) If not then it seems like the base is 26, so I’m not seeing where the 27 multiplier is coming from, except that it’s also a case where there’s no 0 (like music?) and that might throw things off
Edit: Ok, the comment by Morti explains everything. It’s not the blank, it’s the A ≠ AA so there are more numbers before a digit is added thing.
Why would one need to convert the columns to numbers again? And why wouldn’t you just represent that data in a graph instead?
I’ve done some seriously stupid shit in excel, mostly due to it being the only tool I had. By the time I handed the project off to someone else for maintenance/feature creep, there were VLOOKUP ranges spanning dozens of columns. VLOOKUP doesn’t care what column the target is named, only the offset from the beginning of the range. So being able to calculate CA minus W is pretty handy.
Yes, the project should have been a database. But these things happen when skinflint company meets annoyed amateur: you get a sprawling VBA abomination that, despite making actual developers want to choke a bitch, still works orders of magnitude better than the previous system.
