Explanation (which might be wrong, since I’m writing this after banging my head against a wall. Please do correct me if I’m wrong):
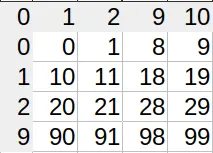
In regular numbering systems (i.e., decimal), we exhaust all 10 digits (0–9) before we reach two-digit numbers. The first number to require 3 digits is 10². The first to use 4 is 10³, and so on.
In music intervals, there is no “0”. The interval c’–c’, for instance, is called a prime (1). This has the funny consequence that moving by a fifth and then by a fourth doesn’t land you on the ninth, but the octave (8). Moving by an octave and then another octave gets you to the 15th, not the 16th.
In Excel, shit hits the fan when you need to convert column names (A, B, C…) to numbers (0, 1, 2…). Since we use 26 characters as our ‘digits’, we’re in the hexavigesimal system. Knowing what I told you in the first paragraph, you’d expect the first double-digit column (AA) to be 26. And you’re right.
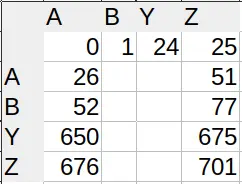
However, when do we need 3 digits? Which column is column AAA? A sane person would say it’s 26², so 676. Ha! No. Column number 676 is actually ZA. What gives? Well, we only ditch the zero for single digit numbers. All subsequent columns actually use 27 different characters, the ‘empty character’ being one of them. That’s where we get the ‘single digit’ – there actually is a second digit, only it’s empty.
So the column AAA actually has index 702, or 26×27. Which index does the column AAAA have? 26×27². The system of adding powers of the base works, only we changed bases midway through.
You can see the lopsidedness in the index lookup table (I’m not displaying all characters for brevity). Sane number systems have square tables. Excel’s is 26×27 (shown are 4×5).
This is worded confusingly. The reason for this is simply because you include the base note when you start counting, so if you stop midway and stack another interval on top, you have to account for that stop because it decreases the total travel distance by one.
This is done to actually increase consistency. If you start at c1 and move up an octave and then move up another octave, you stop at c3 which is logical. So you either move 2 octaves or one 15th because 2*8-1 = 15.
I’m arguing that ‘counting the base note’ is necessary because there is no zero. If you travel 1 unit of your favorite unit of length, stop, and move one unit more, you have moved 2 units, not 3 as it is in music. Stops don’t add to or reduce travel distance.
Name the prime a “none”, the octave a sept.
Now, 2 “septaves”, c1 to c3, are a 14th. 2*7 = 14.
You can make off-by-one intervals work, but you have to constantly juggle some +1s or -1s compared to what we usually use.
If you counted distance in steps, then moving from your front door to your front door would be 0 steps, not one, and moving by 6 steps is twice the distance of 3 steps.
A piano with 5 septaves has 5*7 = 60 keys, wait.
So anyway mathematically one dodecave, one 12th, c1 to c2, has 12 segments, the frequency diffefence is 2. So a second, 2 notes, has 2/12 of that interval, the ratio is 22/12.
A first, a halftone, has 21/12 as its frequency ratio, and a none has 20/12 = 1, the same frequency.
No matter if you count physical keys, distance on a keyboard to change a note by, or mathematical frequency in the air, starting at 1 goes against our intuition, and when you try to add or multiply it is easy to get completely wrong results.
PS: You might want to go C to C on your 5 dodecave keyboard, in which case the concept of “started hour” etc. is familiar, you know to add one arriving at 61 keys, and you know that means an assymetry where one C doesn’t have 11 other keys to itself.
The other way around you’d have to subtract 4, so probably subtract 5 and add 1 since you were dealing with 5 tredecaves in your head not 1 base tredecave followed by 4 extension tredecaves.